Главная > Справочник по математике > Таблица интегралов

Таблица основных неопределенных интегралов

Главные интегралы, которые должен знать каждый студент

Перечисленные интегралы - это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.

Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!

Интеграл от константы

${\displaystyle \int Adx=Ax+C}$ (1)

Интегрирование степенной функции

В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.

${\displaystyle \int xdx=\frac{x^2}{2}+C}$ (2)
${\displaystyle \int x^{2}dx=\frac{x^3}{3}+C}$ (3)
${\displaystyle \int \frac{1}{\sqrt{x}}dx=2\sqrt{x}+C}$ (4)
${\displaystyle \int \frac{1}{x}}dx=\ln \left|x\right|+C$ (5)
${\displaystyle \int \frac{1}{x^2}}dx=-\frac{1}{x}+C$ (6)
${\displaystyle \int x^n}dx=\frac{x^{n+1}}{n+1}+C(n\ne -1)$ (7)

Интегралы от показательной функции и от гиперболических функций

Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.

{\displaystyle \int e^x}dx=e^x+C (8)
${\displaystyle \int a^x}dx=\frac{a^x}{\ln a}+C(a>\mathrm{0,}a\ne 1)$ (9)
${\displaystyle \int shx}dx=chx+C$ (10)
${\displaystyle \int chx}dx=shx+C$ (11)

Базовые интегралы от тригонометрических функций

Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен "минус косинусу", а вот интеграл от cosx равен "просто синусу":

${\displaystyle \int \sin xdx=-\cos x+C}$ (12)
${\displaystyle \int \cos xdx=\sin x+C}$ (13)
${\displaystyle \int \frac{1}{{\cos }^{2}x}}dx=tgx+C$ (14)
${\displaystyle \int \frac{1}{{\sin }^{2}x}}dx=-ctgx+C$ (15)

Интегралы, сводящиеся к обратным тригонометрическим функциям

Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) - частный случай (19).

${\displaystyle \int \frac{1}{1+x^2}}dx=arctgx+C=-arcctgx+C$ (16)
${\displaystyle \int \frac{1}{x^2+a^2}}=\frac{1}{a}arctg\frac{x}{a}+C(a\ne 0)$ (17)
${\displaystyle \int \frac{1}{\sqrt{1-x^2}}}dx=\arcsin x+C=-\arccos x+C$ (18)
${\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}}dx=\arcsin \frac{x}{a}+C=-\arccos \frac{x}{a}+C(a>0)$ (19)

Более сложные интегралы

Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.

${\displaystyle \int \frac{1}{\sqrt{x^2+a^2}}}dx=\ln \left|x+\sqrt{x^2+a^2}\right|+C$ (20)
${\displaystyle \int \frac{1}{\sqrt{x^2-a^2}}}dx=\ln \left|x+\sqrt{x^2-a^2}\right|+C$ (21)
${\displaystyle \int \sqrt{a^2-x^2}}dx=\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \frac{x}{a}+C(a>0)$ (22)
${\displaystyle \int \sqrt{x^2+a^2}}dx=\frac{x}{2}\sqrt{x^2+a^2}+\frac{a^2}{2}\ln \left|x+\sqrt{x^2+a^2}\right|+C(a>0)$ (23)
${\displaystyle \int \sqrt{x^2-a^2}}dx=\frac{x}{2}\sqrt{x^2-a^2}-\frac{a^2}{2}\ln \left|x+\sqrt{x^2-a^2}\right|+C(a>0)$ (24)

Общие правила интегрирования

1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ${\displaystyle \int (f(x)+g}(x))dx={\displaystyle \int f(x)dx+{\displaystyle \int g(x)dx}}$ (25)

2) Интеграл от разности двух функций равен разности соответствующих интегралов: ${\displaystyle \int (f(x)-g}(x))dx={\displaystyle \int f(x)dx-{\displaystyle \int g(x)dx}}$ (26)

3) Константу можно выносить за знак интеграла: ${\displaystyle \int Cf(x)}dx=C{\displaystyle \int f(x)dx}$ (27)

Легко заметить, что свойство (26) - это просто комбинация свойств (25) и (27).

4) Интеграл от сложной функции, если внутренняя функция является линейной: ${\displaystyle \int f(Ax+B)}dx=\frac{1}{A}F(Ax+B)+C(A\ne 0)$ (28)

Здесь F(x) - первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.

Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:

${\displaystyle \int f(x)g(x)}dx=?$ ${\displaystyle \int \frac{f(x)}{g(x)}}dx=?$ (30)

Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ "борьбы" с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже "школьные" формулы алгебры или тригонометрии.

Простой пример на вычисление неопределенного интеграла

Пример 1. Найти интеграл: $${\displaystyle \int (3x^2+2\sin x-7e^x+12)dx}$$

Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем: $${\displaystyle \int 3x^{2}dx}+{\displaystyle \int 2\sin xdx-{\displaystyle \int 7}}{e}^{x}dx+{\displaystyle \int 12dx}$$

Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду

$$3{\displaystyle \int x^{2}dx}+2{\displaystyle \int \sin xdx-7{\displaystyle \int }}{e}^{x}dx+12{\displaystyle \int 1dx}$$

А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:

$$3\frac{x^3}{3}-2\cos x-7e^x+12x+C$$

После элементарных преобразований получаем окончательный ответ:

$$x^3-2\cos x-7e^x+12x+C$$

Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.

Сводная таблица интегралов

${\displaystyle \int Adx=Ax+C}$

${\displaystyle \int xdx=\frac{x^2}{2}+C}$

${\displaystyle \int x^{2}dx=\frac{x^3}{3}+C}$

${\displaystyle \int \frac{1}{\sqrt{x}}dx=2\sqrt{x}+C}$

${\displaystyle \int \frac{1}{x}}dx=\ln \left|x\right|+C$

${\displaystyle \int \frac{1}{x^2}}dx=-\frac{1}{x}+C$

${\displaystyle \int x^n}dx=\frac{x^{n+1}}{n+1}+C(n\ne -1)$

${\displaystyle \int e^x}dx=e^x+C$

${\displaystyle \int a^x}dx=\frac{a^x}{\ln a}+C(a>\mathrm{0,}a\ne 1)$

${\displaystyle \int shx}dx=chx+C$

${\displaystyle \int chx}dx=shx+C$

${\displaystyle \int \sin xdx=-\cos x+C}$

${\displaystyle \int \cos xdx=\sin x+C}$

${\displaystyle \int \frac{1}{{\cos }^{2}x}}dx=tgx+C$

${\displaystyle \int \frac{1}{{\sin }^{2}x}}dx=-ctgx+C$

${\displaystyle \int \frac{1}{1+x^2}}dx=arctgx+C=-arcctgx+C$

${\displaystyle \int \frac{1}{x^2+a^2}}=\frac{1}{a}arctg\frac{x}{a}+C(a\ne 0)$

${\displaystyle \int \frac{1}{\sqrt{1-x^2}}}dx=\arcsin x+C=-\arccos x+C$

${\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}}dx=\arcsin \frac{x}{a}+C=-\arccos \frac{x}{a}+C(a>0)$

${\displaystyle \int \frac{1}{\sqrt{x^2+a^2}}}dx=\ln \left|x+\sqrt{x^2+a^2}\right|+C$

${\displaystyle \int \frac{1}{\sqrt{x^2-a^2}}}dx=\ln \left|x+\sqrt{x^2-a^2}\right|+C$

${\displaystyle \int \sqrt{a^2-x^2}}dx=\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \frac{x}{a}+C(a>0)$

${\displaystyle \int \sqrt{x^2+a^2}}dx=\frac{x}{2}\sqrt{x^2+a^2}+\frac{a^2}{2}\ln \left|x+\sqrt{x^2+a^2}\right|+C(a>0)$

${\displaystyle \int \sqrt{x^2-a^2}}dx=\frac{x}{2}\sqrt{x^2-a^2}-\frac{a^2}{2}\ln \left|x+\sqrt{x^2-a^2}\right|+C(a>0)$

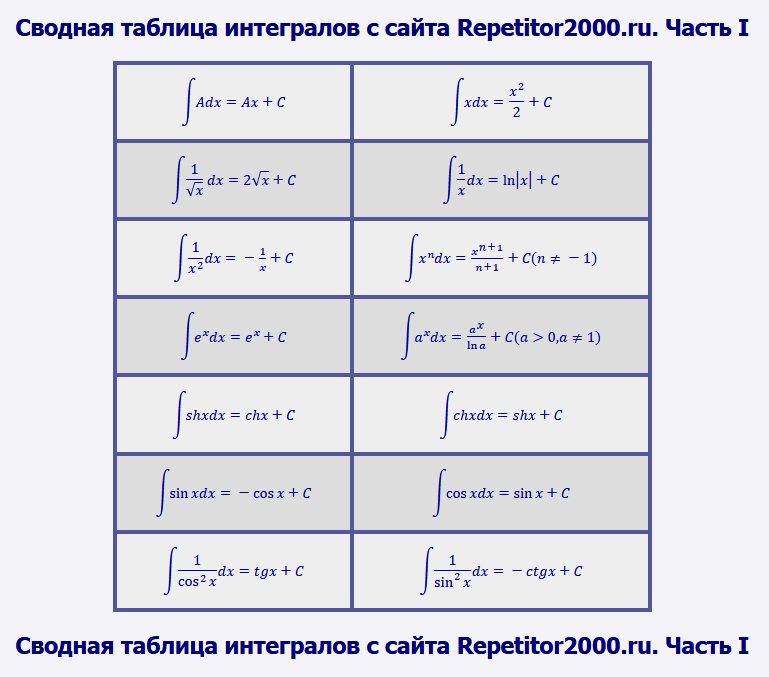
Скачайте таблицу интегралов (часть I) по этой ссылке


Скачайте таблицу интегралов (часть II) по этой ссылке

Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!

Возможно, вас заинтересуют также